Binary tree traversal
Page content
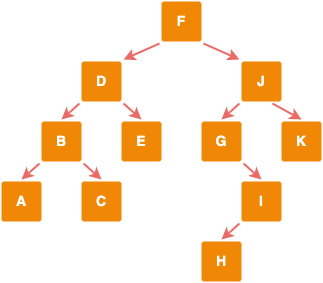
1. Breadth-First Search Algorithm
Level 0 -> Level 1 -> … -> Level n
F D J B E G K A C I H
BFS Implementation: Recursive (Python)
class Node:
def __init__(self, val):
self.left = None
self.right = None
self.val = val
class Tree:
def __init__(self, root):
self.root = Node(root)
def height(root):
if root:
return max(height(root.left), height(root.right)) + 1
return 0
def visit_level(root, level, visited):
if root:
if level == 1:
visited.append(root.val)
else:
visit_level(root.left, level-1, visited)
visit_level(root.right, level-1, visited)
def bfs(root):
visited = []
for level in range(1, height(root)+1):
visit_level(root, level, visited)
return visited
if __name__ == "__main__":
tree = Tree('F')
tree.root.left = Node('D')
tree.root.left.left = Node('B')
tree.root.left.left.left = Node('A')
tree.root.left.left.right = Node('C')
tree.root.left.right = Node('E')
tree.root.right = Node('J')
tree.root.right.left = Node('G')
tree.root.right.left.right = Node('I')
tree.root.right.left.right.left = Node('H')
tree.root.right.right = Node('K')
print("BFS:")
print(f"Level order: {bfs(tree.root)}")
2. Depth-First Search Algorithm
2.1. Preorder
Root -> Left -> Right
F D B A C E J G I H K
2.2. Inorder
Left -> Root -> Right
A B C D E F G H I J K
2.3. Postorder
Left -> Right -> Root
A C B E D H I G K J F
DFS Implementation: Recursive (Python)
class Node:
def __init__(self, val):
self.left = None
self.right = None
self.val = val
class Tree:
def __init__(self, root):
self.root = Node(root)
def preorder(root, visited):
if root:
visited.append(root.val)
visited = preorder(root.left, visited)
visited = preorder(root.right, visited)
return visited
def inorder(root, visited):
if root:
visited = inorder(root.left, visited)
visited.append(root.val)
visited = inorder(root.right, visited)
return visited
def postorder(root, visited):
if root:
visited = postorder(root.left, visited)
visited = postorder(root.right, visited)
visited.append(root.val)
return visited
if __name__ == "__main__":
tree = Tree('F')
tree.root.left = Node('D')
tree.root.left.left = Node('B')
tree.root.left.left.left = Node('A')
tree.root.left.left.right = Node('C')
tree.root.left.right = Node('E')
tree.root.right = Node('J')
tree.root.right.left = Node('G')
tree.root.right.left.right = Node('I')
tree.root.right.left.right.left = Node('H')
tree.root.right.right = Node('K')
print("DFS:")
print(f"Preorder: {preorder(tree.root, [])}")
print(f"Inorder: {inorder(tree.root, [])}")
print(f"Postorder: {postorder(tree.root, [])}")